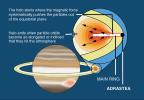
The top and bottom panels show a mosaic of images of Jupiter's rings taken by NASA's Galileo spacecraft. Jupiter is to the right of this mosaic, and different brightness scales accent different parts of the ring system. Jupiter's ring system has three parts -- a flat main ring; a halo inside the main ring shaped like a double-convex lens; and the gossamer ring outside the main ring. In the top view, a faint mist of particles is seen above and below the main ring. This vertically extended "halo" is unusual in planetary rings, and is caused by electromagnetic forces pushing the smallest grains, which carry electric charges, out of the ring plane.

Development of Jupiter's Main Ring and Halo

Jupiter's main ring is a thin sheet of material encircling the planet. The near and far arms of this ring extend horizontally across the mosaic, joining together at the ring's ansa, the portion visible on the sides of Jupiter, on the figure's far left side. In the bottom view, some radial structure is visible across the ring's ansa. The diffuse innermost boundary begins at approximately 122,500 kilometers (about 76,100 miles). The main ring's outer radius is at about 128,940 kilometers (80,120 miles), very close to the orbit of the Jovian moon Adrastea (128,980 kilometers or 80,140 miles). The brightness of the main ring drops markedly at about 127,850 kilometers (79,440 miles), very near the orbit of another moon, Metis, at 127,978 kilometers (79,521 miles). Jupiter's four small satellites, Metis, Adrastea, Amalthea and Thebe, affect the structure of the huge planet's tenuous rings.

Jupiter's Main Ring and Halo

These images were taken through the clear filter of Galileo's onboard solid state imaging camera system on November 9, 1996. The resolution is approximately 24 kilometers (14 miles) per picture element along Jupiter's rings. Because the spacecraft was only about 0.5 degrees above the ring plane, the image is highly foreshortened vertically. The images were obtained when Galileo was in Jupiter's shadow, peering back toward the Sun, when the ring was approximately 2.3 million kilometers (1.4 million miles) away. The view of Earth's moon in the explanatory graphics was created from images returned by the Clementine lunar orbiter, launched in 1994 by NASA and the Ballistic Missile Defense Organization.

JPL manages the Galileo mission for NASA's Office of Space Science, Washington, DC.

The images are posted on the Internet at https://photojournal.jpl.nasa.gov/ and at http://galileo.jpl.nasa.gov.

Background information and educational context for the images can be found at: http://www.jpl.nasa.gov/galileo/sepo.